Motion Illusions

There have been a lot of visual motion illusions going around Twitter recently. I think it is super cool that people find these motion demos so compelling. However, I’ve been surprised to see lots of claims that there is “no motion” in the illusions and most people seem to think there’s some perceptual magic going on.

What is this magic?

For example, this crazy mario illusion

The marios look like they’re moving throughout the level, but each mario never gets anywhere. It’s really quite upsetting.

A number of people have expressed wonder at this example, pointing out that “nothing is actually moving”.

And it follows in a whole series of really clever illusions that use the same effect, but are often designed to mislead the observer.

How do these illusions work?

I thought this was a good opportunity to write up a little blog post about visual motion. Let’s take this Mario example here and look at what’s actually going on.

But first, what is motion?

Motion is change in position over time.

Something that does not move is static because it has the same position as time progresses. We often think of motion in the real world: furniture does not change position over time (does not move). You, your dog, all animals, your limbs, all change position over time. So, they move in the world.

However, from the perspective from your visual system (or a video camera), motion isn’t so straightforward. For example, if I were to pan a camera across a room, the room would be moving with respect to the reference frame of the camera. That is motion as well. In other words, visual motion is not just a result of things moving in the world, but can also result from the sensor moving.

So, what is visual motion and how do we see it? Let’s take the idea of something changing position over time in the real world and apply it to the pixels of a movie. You’ll see this makes sense in a minute. Here’s a video of a real moving thing swinging.

from Giphy

What makes this a video of a moving thing? Well, if we look at different frames, we can see the position of the orangutan has moved over time.

That tells us that the orangutan has moved, even with a fixed reference frame (the camera has not moved). Therefore the orangutan has moved in the real world.

One way to visualize this would be to plot the pixel values over time to see how they change. Since we cannot plot every frame at all time points, let’s take a slice through space and look how that slice changes over time. You can move your mouse (scrub) over the 2D image frame to see different space-time slices.

Scrub over the space-time slice to play through time in the movie. It won’t be intuitive at first, but there is a mapping from the motion of objects in the images to the patterns in the space x time slices. Specifically, motion is orientation…

Track the body of the orangutan and the branch. You can see that the movement of the orangutan and the branch form slanted structure in the space-time plots, whereas the background looks like vertical streaks.

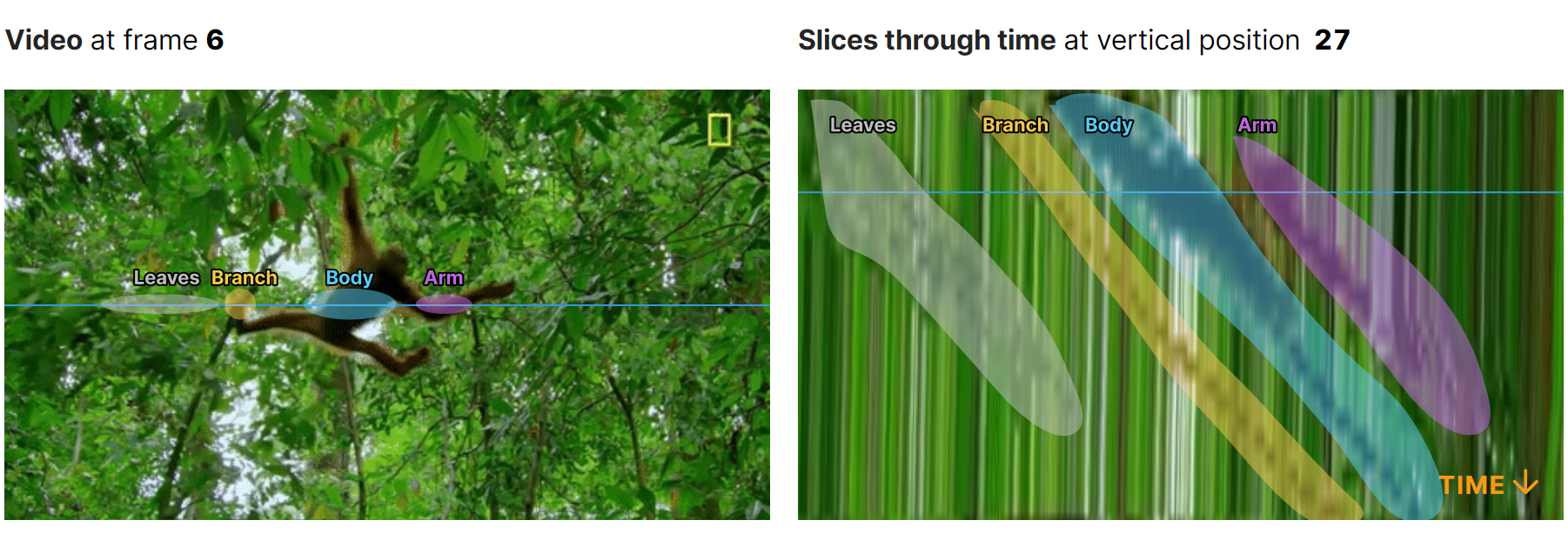
It’s a little tricky to see at first, but it’s clear which things are moving and which are not. All of the slanted (or “oriented”) stuff in the space-time slice is stuff that’s moving. In other words, we can define “Visual Motion” as orientation in space-time.

• Vertical structure in space-time does not move.

• Horizontal structure in space-time, such as the edge of the leaves here, are appearances and disappearances.

The TLDR of this whole post is: Our visual system detects orientation in space-time to see motion using little local detectors.

But before we get into that, what’s happening with the Marios? Is there orientation there as well?

What’s happening with the marios?

Above, we built a quick intuition for how visual motion is really just orientation in space-time. Let’s zoom in on a single Mario to see what happens if we use the same trick. Here is a single mario. It appears to be moving to the right, but it never leaves the frame. This is the essential component of the illusion.

If we take a slice through this mario, we can use the intuitions we learned above to see what’s going on. In this figure, time is running up.

First, the mario is flashing different colors. That appears as horizontal rainbow-colored lines. Horizontal structure in space-time plots (where time runs up or down) is something appearing or disappearing (or, flashing!).

Second, in this view, we can clearly see where the motion comes from. There is oriented structure on the edges of the marios. Although there is a hard edge between the colors and the gray that is vertical (and therefore does not move), the colors are oriented at the edge.

The color has nothing to do with the illusion - let’s rid of it for now because it’s just a distraction. Here you’ll see the same Mario in grayscale (I’ve just averaged across the color channels) and you can still see the effect.

From here, we can construct a really simple illusion that follows the same principles. We’ll build an image that represents space-time and then play it back as a 2D movie.

The image I’ll make here is constructed using the same principle as the Mario’s edge. The center is modulated in brightness, just like the Mario’s color was modulated. The edges drift to the right for 5 frames and then jump back to the start. At each jump, the sign inverts and the cycle starts again. Before scrolling down, try to imagine what this looks like if we played it as a movie.

Since there is only 1D space in our image from above, we don’t have a 2D image at each time point. But, we can visualize that 1D info as vertical bars.

Here’s a single frame of our new illusion.

And here’s the full movie of our space-time constructed object.

If we look back at the space-time construction again, we can see something interesting. There is an edge moving to the right, but it keeps jumping back and changing sign (white is on ones side and black on the other and then it flips).

But we keep seeing motion to the right. This tells us something: our visual motion system doesn’t care about the sign of that edge. The lingo that vision scientists use to talk about this is motion perception doesn’t care about phase (for the purposes of this blog post, phase is just the exact sign and position of that edge).

In other words, motion perception only cares about the orientation, not the stuff it’s made of. And that’s pretty neat.

Next, let’s look at an old model of visual motion processing with this property.

The motion energy model

Let’s look at the state-of-the-art in human motion perception (in the mid 1980s), also known as the ”motion energy model”. This is really a beautiful paper, so I recommend anyone interest click in and take the time to read it. Also, not all that much has changed in our understanding of the fundamentals in the last 35 years.

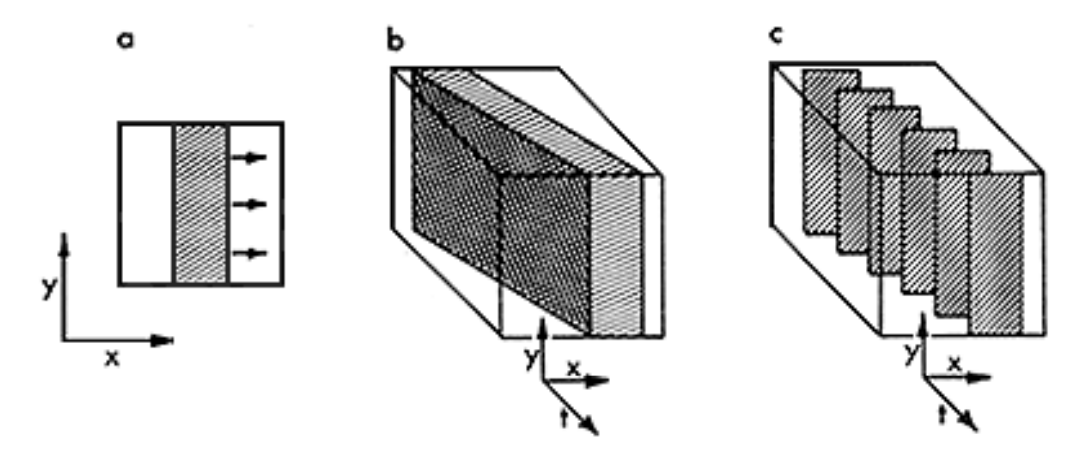
So, how does human motion detectors work? Adelson and Bergen start by making the same point that was demonstrated above: visual motion is orientation in space-time. Panel a shows a frame of a movie with a bar moving to the right (like our orangutan, above). b shows the full spatiotemporal volume of the bar moving through space and time as if it were continuously moving. But, of course, movies have frames and a frame rate. Panel c shows the same volume, but now it reflects the frame rate of a movie.

From here, it makes sense to think about how to build detectors for motion. The picture below shows that if you had an oriented filter in space time, you could detect the edge. For the non-scientists reading this, you can think of these filters like little “edge detectors”. These types of oriented filters are decent enough descriptions of the responses of neurons in visual cortex. For example, here’s a link to a video of what Hubel and Wiesel found in their classic experiments on primary visual cortex, which they concluded looks like a little line (or edge) detector.

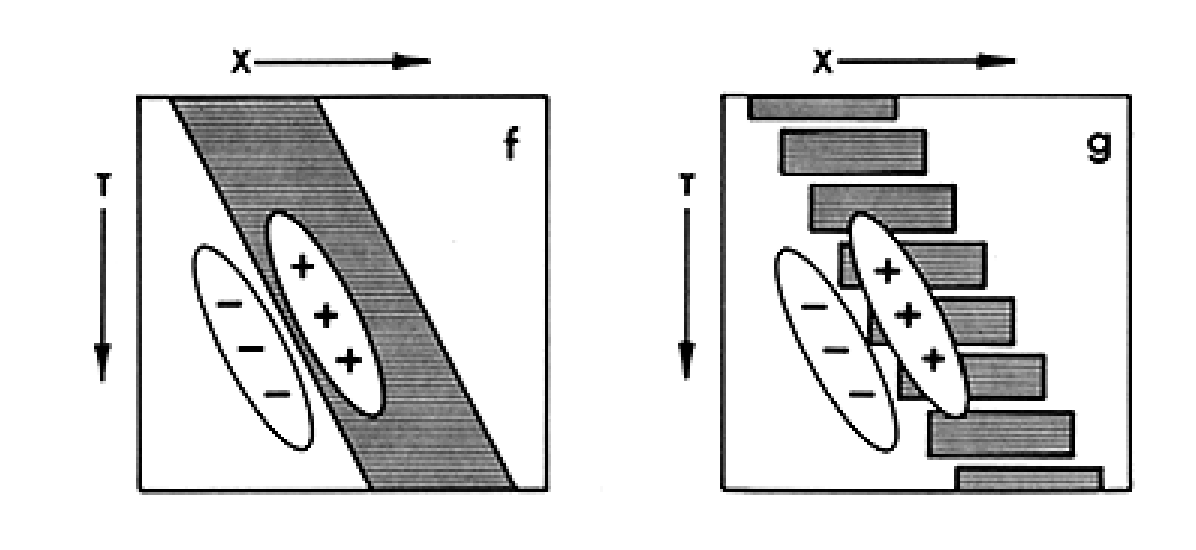Importantly, these edge detectors still care about the sign of the edge. This, as we noted above, is unlike our percept. To build detectors that do not care about phase (don't care about the polarity of the edge). We can combine two oriented filters that care about opposite signs. In technical terms, these filters are 90° out of phase, forming a "Quadrature Pair". Really don't worry about that jargon. This just means that where one filter _likes_ white, the other _likes_ black (and vice versa).

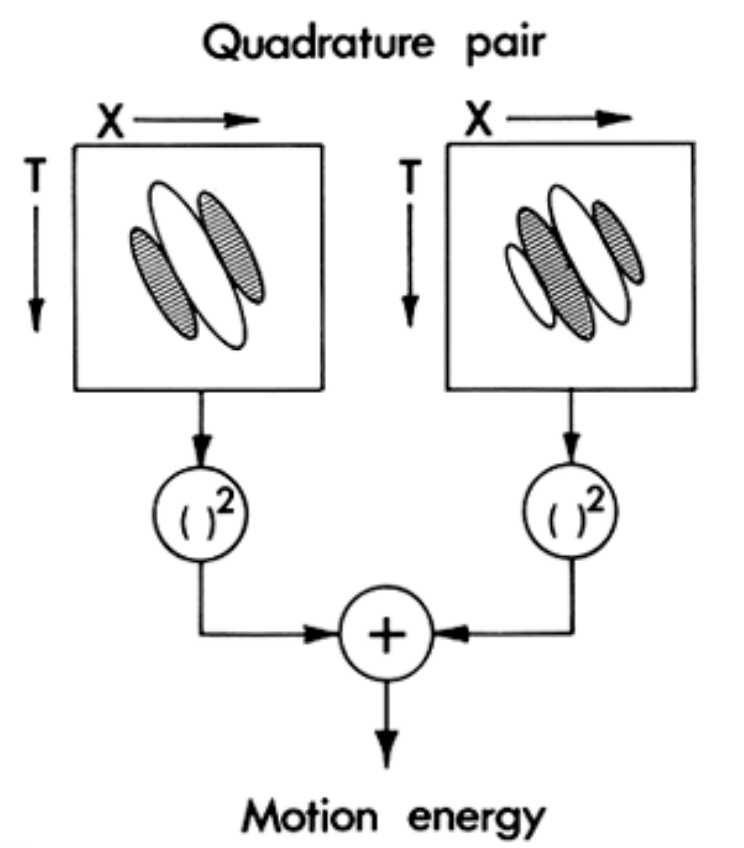
Note: A very related paper from Watson and Ahumada came out in the same year and covers many of the same points.

Using the equations from Adelson and Bergen, 1985, we can make the same little motion energy filters. Note: in my visualization below, time runs up.

The two filters on the right are selective to and edge moving to the right and are 90° out of phase with eachother. The two filters on the left are selective to a leftward moving edge and are 90° out of phase with each other.

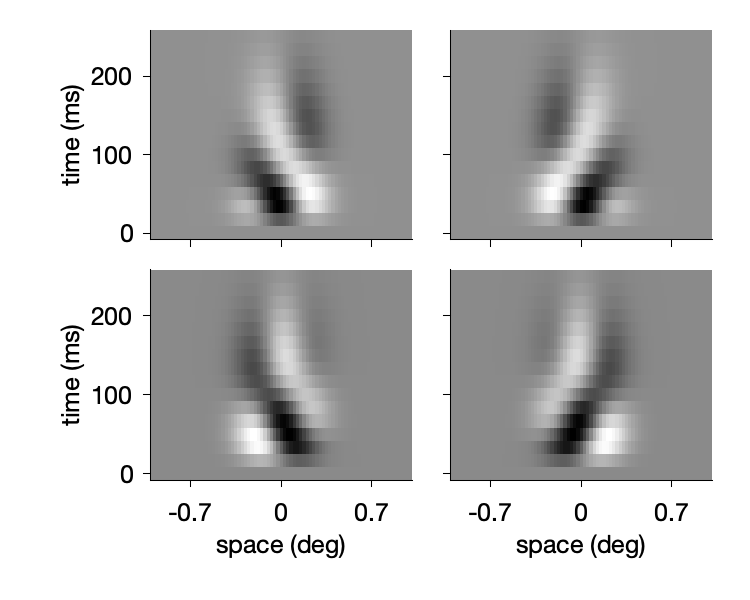
Here’s a movie of what these look like:

Let’s pause for a second here and take note of two things:

1. These little movies look a lot like what the edges of the marios do. So, contrary to the claim that the marios are “not moving” they are, in fact, made up of the fundamental elements of motion.
2. Derivatives

What? Derivatives?

How did Adelson and Bergen make these little moving edge detectors? Well, the key underlying component is the concept of a derivative. The spatial selectivity of these filters was created by taking the 1st and 2nd derivatives of a Gaussian.

The first idea to get across is that derivatives detect change (that’s basically the definition). The derivative of a function $\frac{\partial }{\partial x}f(x)$ is how much the function value ($f(x)$) changes for really small changes in $x$. That $\partial x$ just means “tiny changes in x”.

Intuitively then, something that moves will have to change as a function of changes in space, $\partial x$, and time, $\partial t$. A derivative filter is designed to detect those changes. And we can make a smooth one by starting with a smooth,localized, function and taking its derivative.

A Gaussian is a smooth bump spatially and taking the derivative can create the type of edge detector that Adelson and Bergen wanted to make. Here’s what that looks like. Note: I’ve normalized both curves to have the same amplitude.

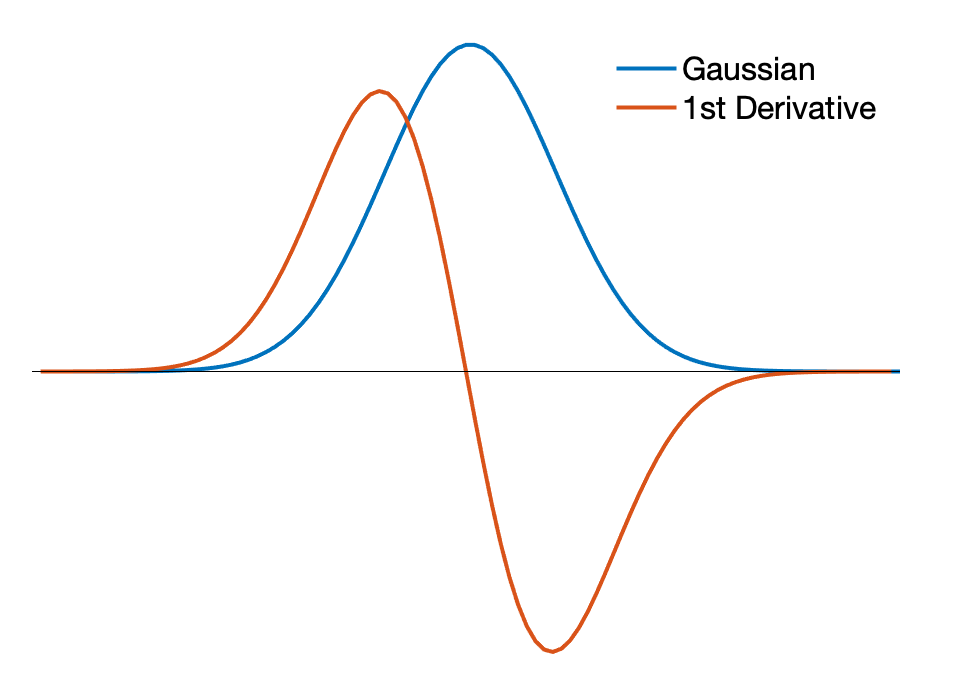
So, one way to make a little “edge detector” is a derivative filter. Thinking of early vision in terms of little derivatives is really useful.

Motion Energy Model on “the Marios”

So, is there motion in “the Marios” illusion? Let’s use the motion energy model to find out. Below, I’m going to play a movie of the cropped mario with the output of the motion energy model colored by the cardinal directions (using the following colors)

Remember, the Mario we cropped looked like it was moving to the right.

And the motion energy model agrees: Mario is moving to the right.

We can see a couple cool things from this movie:

1. Rightward motion is only detected along the vertical edges. This is consistent with a principle that motion can only be encoded in the direction perpendicular to the orientation of an edge.
2. There is some detected motion upwards and downwards at the top and bottom of the marios. This is also consistent with the point about edges made above.

Our local motion detectors can’t integrate motion over large parts of space, so they only “see” the local signals at edges.

Let’s look at what happens with the full Mario illusion:

The motion energy model agrees (mostly) with our percept of the Marios. One issue visualizing it this way is that the colors mask the edges which kills the illusion. So, let’s just look at the average motion energy over time:

Conclusions

Alright, so now that we took this whirlwind tour of visual motion perception applied to motion illusions. What did we learn?

1. Visual Motion can be thought of as orientation in space-time

Because motion is defined by changes in space over time, it will appear as oriented structure when looking at space-time slices of a movie.

2. Human motion perception works by integrating across little motion detectors that do not care about phase

We see the marios as “moving” because they are. They are made of little space-time oriented elements at the edges. Our visual system detects those little local motion elements elements and does not care about the polarity of the edge as it moves (which is why the flashing of the marios doesn’t disrupt the perception of constant motion).

3. We can make simple motion detectors that have the properties of human vision

The Adelson Bergen “Motion Energy Model” showed us a simple way to construct motion detectors that don’t care about the polarity of an edge.

4. The motion energy model “sees” motion in the marios just like we do

When we ran the motion energy model on the mario stimulus, those filters from the 1980s predict the same motion that we see. I’d say this a different way. The marios are constructed using these fundamental elements of motion. So, yea, they’re totally moving. They just aren’t going anywhere. And, yes, I know what people mean when they say “nothing is moving”.

5. Human vision relies on change

The motion energy filters we made were constructed using derivative filters. Derivatives are all about change. A large change in space is an edge. A large change in time is an appearance or disappearance. A change in both space and time is motion. Early vision mostly measures changes. That means your perception is going to be dependent on signals that are reflecting changes.

Finally, some interesting perspectives on Twitter…

Some other people have pointed out the strong effect of the edges for seeing object motion.

I think another way of saying this is that early vision works with derivatives, and high-level vision can only integrate those signals. So it kinda makes sense that high-level percepts would depend so much on edges.

Additionally, some people report being able to modulate whether they see the motion or not.

I’m not quite sure about the interpretation regarding “sense of self”, but I can also modulate how big the effect is. One trivial way to do this is to move my eyes to different locations. If I look well off the marios, there is no perceived motion. But that’s not what this Tweet was about.

If I try hard enough (and I’m not sure exactly what I’m doing), I can get the effect to go away. I have two ideas about this. The first is that maybe I’m doing something weird with my fixational eye movements or accommodation. The second option is that I’m playing with my attentional readout of the low-level sensory signals. There’s no getting around what’s in the video (there is motion energy), so to be able to modulate this has something to do with how it’s integrated.

Update: Does Flownet2 match our perception?

Flownet2 is the latest version of Deep Learning’s answer to optic flow. For our intents and purposes here optic flow just means visual motion. The paper describing the model is here and NVIDIA have kindly provided a pytorch implementation. I haven’t had much time to play with the full model, and I’m currently limited to frame width that cropped my original video, but it’s already producing interesting and VERY different output than Adelson Bergen.

Here’s a video visualizing the optic flow produced by FlowNet2 in the mario illusion and comparing that to Adelson Bergen:

First off, flownet looks beautiful, but it totally fails to capture the illusion. I haven’t had a chance to try other versions of the model, but this is not a win for modern machine learning. Adelson Bergen, on the other hand, captures the perceptual effect well. I think I’ll do a deep dive into flownet in the future and see whether there is evidence for phase invariance, or why it is so blobby and full of flicker. Anyway, for now, it’s nice to see that such a simple model from the 1980s performs so well on this “task”. Makes you wonder whether building in some of these principled constraints would make flownet match human perception more closely.