Reconciling Generative and Feedforward Models of Visual Cortex

What is feedback for?

Ask a random Neuroscientist and you’ll get an opinionated answer. Feedback is like pinapple on pizza, everyone has an opinion – and its typically a strong one. The problem, we’re told, is that we don’t understand it. The second problem is people believe wildly different things about what the empirical evidence supports. On the one hand, you have people who think feedback is the main story. The brain, they say, is a generative model. “Perception is a controlled hallucination”. They point to fMRI studies showing huge effects of cognition on early sensory areas. They interpret the smallest changes in firing rates as the tip of a much larger iceberg, “if only we could understand it”. I think this is feedback mania. I used to have it too, back when I was a young grad student before it was beaten out of me. The problem with feedback mania is it leads the field to latch on to any result that suggests there’s a large effect. It’s why the field went so crazy for mouse locomotion – the first time there was a large effect of feedback (I will write separately about that one).

In contrast, the vast majority of empirical evidence at the level of single neuron spiking suggests that feedback is a small modulatory effect. In what is referred to as “the standard model”, neurons in visual cortex (and other sensory areas) are primarily feedforward recurrennt neural networks with some modulatory gain fedback. The standard model is pretty bomb proof empirically. Moreoever, whenever a big feedback effect appears, it’s usually only 5 years or so before the standard model camp designs a careful experiment to control for some overlooked confound and invariably finds that the big feedback effect is just not there. What remains is a consistent small modulatory effect.

In this blog post, I argue that we might be closer to understanding feedback than we thought. I take the stance that indeed the brain learns a generative model of the senses, and perception is inference over the states of that model. But, I argue the standard model is the answer to what that inference looks like.

How can we reconcile the idea of perception as inference with the primarily feedforward processing we see in the brain?

What do I mean by “inference” over a “generative model”?

Perception: Illusions and inference

Let’s start with perception. The idea that our brain actively interprets sensory information, rather than passively receiving it, isn’t new. In fact, it’s ancient. Almost a thousand years ago, the scientist Ḥasan Ibn al-Haytham (a.k.a. Alhazen) proposed that vision involves judgment and inference. Fast forward to the 1870s, and we find the physicist and polymath Hermann von Helmholtz articulating a similar idea more formally. Helmholtz suggested that perception is a process of unconscious inference—our brain’s best guess about what’s out there in the world.

What exactly does that mean? Why can’t we just “see” the senses? Well, illusions are a good way to get an intuition that the brain actively interprates sensory datae, so let’s take a quick tour of some classic visual illusions.

The rotating mask illusion

Lightness from above

Although all the circles in this image are flat with a gradient on them, you, like me, probably percieve them as either convex bumps or concave holes. And the ones with lighter shades on top look like bumps while the ones with lighter shades on the bottom look like holes. This, it is taught, is because the brain assumes that light comes from above and interprets the shading accordingly.

The Bayesian Brain

“Perception is our best guess as to what is in the world, given our current sensory evidence and our prior experience.” - Hermann von Helmholtz

A lot of these illusions can be explained by suggesting that the brain infers something about the world given the senses. The brain does not only process the feedforward sensory data (which is high dimensional and often ambiguous), instead it integrates prior knowledge about the structure of the world to “make sense” of the senses. For example, the prior knowledge that faces are never concave inverts the percept of mask. Similarly, the prior knowledge that light typically comes from above and casts shadows leads to the interpretation of the circles as bumps. How do we formalize? Bayes rule does just that.

The sensory data coming is forms the likelihood (the probability of the sensory data given some state), which is combined with the prior (probability of the state) to support the percept, which is really about the state of the world and not the sense data directly.

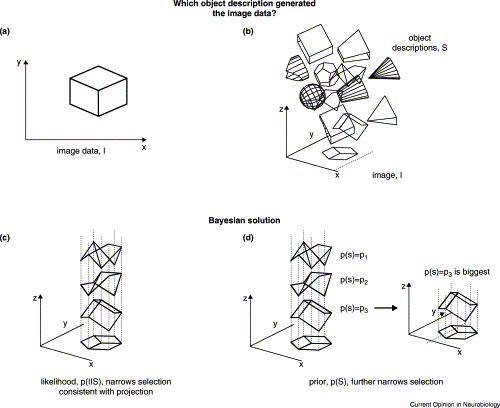
This picture from this review demonstrates the idea nicely. The sensory data shown in the top left is a 2D projection of a 3D shape. This is ambiguous. Many possible 3D objects could project to this exact 2D form. However, most of those are unlikely. The prior probability of the different 3D shapes is combined with the ambiguous 2D image to support our percept of a cube.

How does this happen in the brain?

I don’t want to pretend that neuroscientists don’t have ideas about this, they do. There are many ideas and we’ll get to them below. What I want to emphasize is that “the standard model” of visual processing at the neuronal level – the one you find in textbooks – looks quite different.

The standard model (an overly brief history)

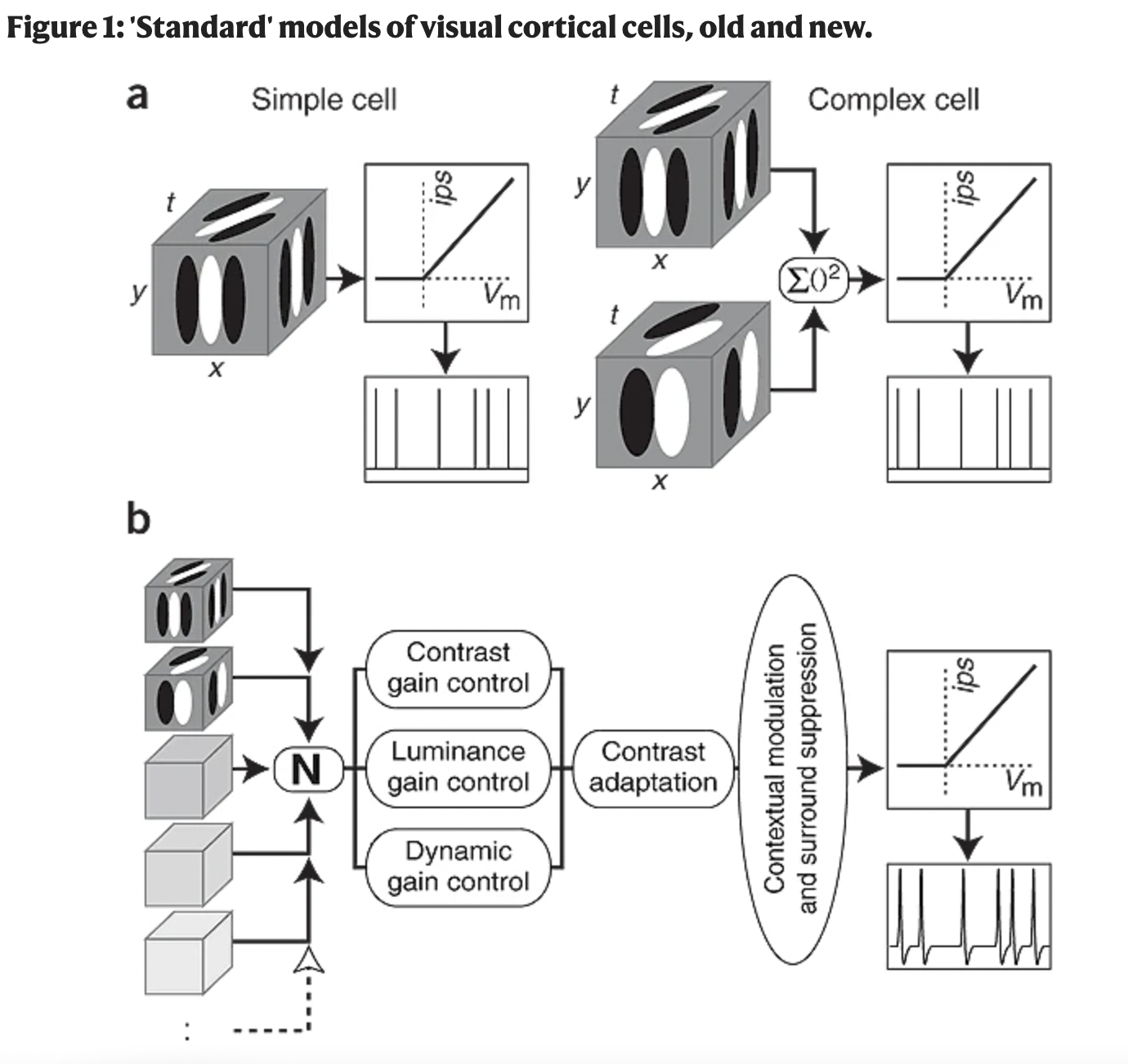
The “standard model” of visual processing is a series of linear-nonlinear cascade of processing stages, which was developed starting in the 1970s. This figure depicts the computational framework for understanding “simple” and “complex” cells (we’ll get to those) as well as additional nonlinearities that are present. These additional nonlinearities are typically captured with a divisive normalization (we’ll get to that) step at each stage. Further work has added in and some extra-retinal gain from things like attention (that can also be modeled as part of divisive normalization). This model remains a really good model of visual cortical areas.

Origins with Hubel and Wiesel: receptive fields and feature extraction

Vision research got a big boost in the 1960s with the pioneering work of Hubel and Wiesel. I’ll write about the importance of this work for the development of convolutional neural networks (CNN) separately, but prior to Hubel and Wiesel, people didn’t really know what to expect in cortex. They knew that neurons in the retina had “receptive fields” (localized light-sensing regions) and they knew that these neurons projected to the lateral geniculate nucleus (LGN) of the Thalamus and then to primary visual cortex (V1). But from that point on, all bets were kind of off. Lashley, for example, thought that primary visual cortex would hold engrams. Hubel and Wiesel’s results showed definitively that this was not the case. Neurons in V1 had receptive fields, and they were organized in a way that suggested a hierarchy of feature extraction. They identified two fundamental classes of V1 neurons: “simple” cells, which responded to oriented edges in a luminance-dependent manner, and “complex” cells, which responded to oriented edges regardless of their position in the receptive field or polarity of light. For those of you who have not seen it, I recommend watching this video (with the sound on) demonstrating the selectivity of V1 neurons.

Hubel and Wiesel used simple wiring diagrams to form a model of how V1 neurons might build new selectivity from their inputs.

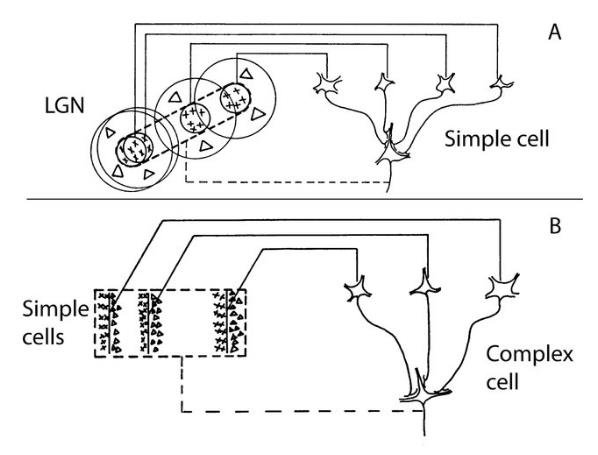
In this classic figure, they demonstrated that what they called “simple” cells in V1 could be built out of LGN-like inputs, and that “complex” cells could be built out of simple cells. This observation lead directly to the development of the first CNN. I also think it is the foundation for neuroscientists’ affinity for naming things (e.g., “Face” cells, “Jennifer Aniston” cells, etc.). I genuinely believe it is the single most important discovery in all of neuroscience to-date and I will write about that separately.

Movshon and the development of the “standard model”

In the 1970s, Tony Movshon and colleagues formalized computational principles that could capture the response properties of simple cells. They showed that under a range of conditions, simple cells could be understood as linear filters followed by a static rectifying nonlinearity (a half-wave rectification). Complex cells, in contrast, “exhibit gross nonlinearities”, which were later formalized as either a max-pooling or an energy operation. Throughout the 80s, many scientists, including (but not limited to) Duane Albrecht, Russ DeValois, and Ralph Freeman charted out the substantial additional nonlinearities such as contrast gain control, surround suppression, and cross-orientation suppression. In the early 1990s many of these nonlinear observations were captured under a single divisive nonlinear operation, which is now known as divisive normalization. Interestingly, Bill Geisler and David Heeger came up with a very similar model at about the same time to capture contrast gain control. I wonder how many others were barking up the same tree.

The 2000s brought more modern machine learning and statistical techniques to allow these models to be fit directly to data, and the 2010s saw the emergence of data-driven and goal-driven deep neural networks to understand cortical neurons. All the while, more and more extra-retinal signals were added to the model, including attention, decision, and motor signals.

The standard model comes from and elegant systems-identification approach to understanding the brain, which is appealing to the engineering-minded neuroscientists. Non-engineers (i.e., biologists, psychologists, and physicits who found themselves studying brains) tend to dislike the standard model. Mainly because it’s not a brain (which is fair) – it’s a function approximation to neurons, and they don’t like that. However, I also think they don’t like that it’s better at predicting neurons than anything they came up with. I will grant them point one, which is what this blog post is about. It’s hard to understand how simply stacking these computations on top of each other will give us a brain, even if it’s a decent function approximation to visual cortical neurons. The standard model tells us how to describe neurons, but it does not tell us why or how exactly.

Problems with the standard model?

So we have two perspectives: perception as inference, and vision as passive (albeit adaptive) filtering. Both are supported by evidence. Both have led to important insights and technological advances. Do they fit together?

On the one hand, yes they do. The standard model camp have demonstrated time and time again that Bayesian-like perception can be explained with the distribution of selectivity where the perception and physiology match. Feed-forward population codes were shown to be able to do Bayesian integration where, again, the perception and physiology match. To be fair to the standard model, it is a very successful model of visual processing AND it can be integrated into Bayesian models of perception. I’d note that on this point, amortized inference does just this: inference with feedforward networks. This is the foundation of variational autoencoders and other deep generative models. In some simple ways, “feedforward” and “inference” can be made to work together.

On the other hand, many neuroscientists want a more direct reconciliation of the two perspectives. They want to see the brain doing inference, not just filtering. They want to see neurons actively predicting and comparing those predictions to sensory input. They want to see the brain as a generative model, not just a fancy filter. They want to find some actual computational role for all those feedback connections.

Additionally, the “standard model” is fundamentally a descriptive model. It is a description of what computations neurons are doing, not a normative model of what they should be doing or how they got there. It’s also not a mechanistic model. It doesn’t tell us how to build neurons biopysically. As a result, it isn’t really a model of a brain. At best, it gives us p(spike|stimulus, everything else) and there are reasons as scientists we might want more than that.

Predictive Coding

Probably the most famous example of an attempt to reconcile the two perspectives (Perception as inference and Neurons as adaptive filters) under one theory is predictive coding, which has been applied widely in neuroscience and now machine learning. This fundamentally flips the direction of emphasis in the brain from feedforward to feedback. In predictive coding, the brain is fundamentally a prediction machine and feedback connections carry samples from a generative model. The general idea is clearly articulated in Rajesh Rao and Dana Ballard’s 1999 paper.

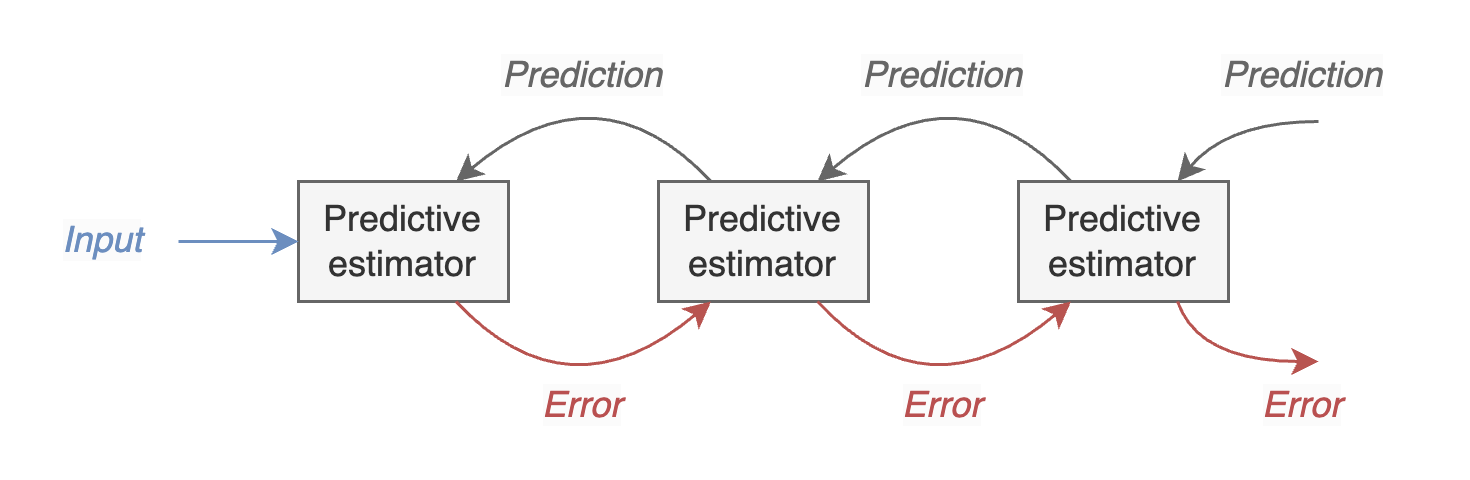
The figure (reproduced from here ) shows the general framework of predictive coding, which posits neurons in sensory cortex perform hierarchical inference over a generative model with top-down connections carrying predictions and feedforward signals carrying prediction errors. The claim is that neurons in visual cortex can be understood “as residual error detectors, signaling the difference between an input signal and its statistical prediction based on an efficient internal model of natural images”. In otherwords, adaptive filters result from inference over a model of natural images and depend fundamentally on detailed predictions that are fed back through the hierarchy.

This approach “flips the system around”. Brains beome “prediction machines” and individual neurons are part of a generative model. What is a generative model? One way of putting is that vision is just inverse graphics. The brain has an internal mdodel of the world and when new light comes into the eyes, it infers what about its model caused that light.

The problem

Predictive coding is a powerful framework, with a huge caveate: there is very little direct evidence for current versions of it over the standard model. What I mean by that is that neuroscientists have not found good evidence for feedback consistent with detailed predictions. Instead, they repeatedly find empirical observations that are consistent with something that looks a lot like the standard model with some modulatory feedback.

I don’t want to spend an entire post on the limited evidence for explicit predictions, but the short version is that all the effects observed by proponents of the theory can also be explained by feed-forward models. There is a nice discussion of this here. Let’s say you don’t buy it yet. I’ll remind you that the retina does many forms of prediction without feedback and that feedforward CNNs trained to predict retinal spikes from natural movies also mimic these predictive behaviors.

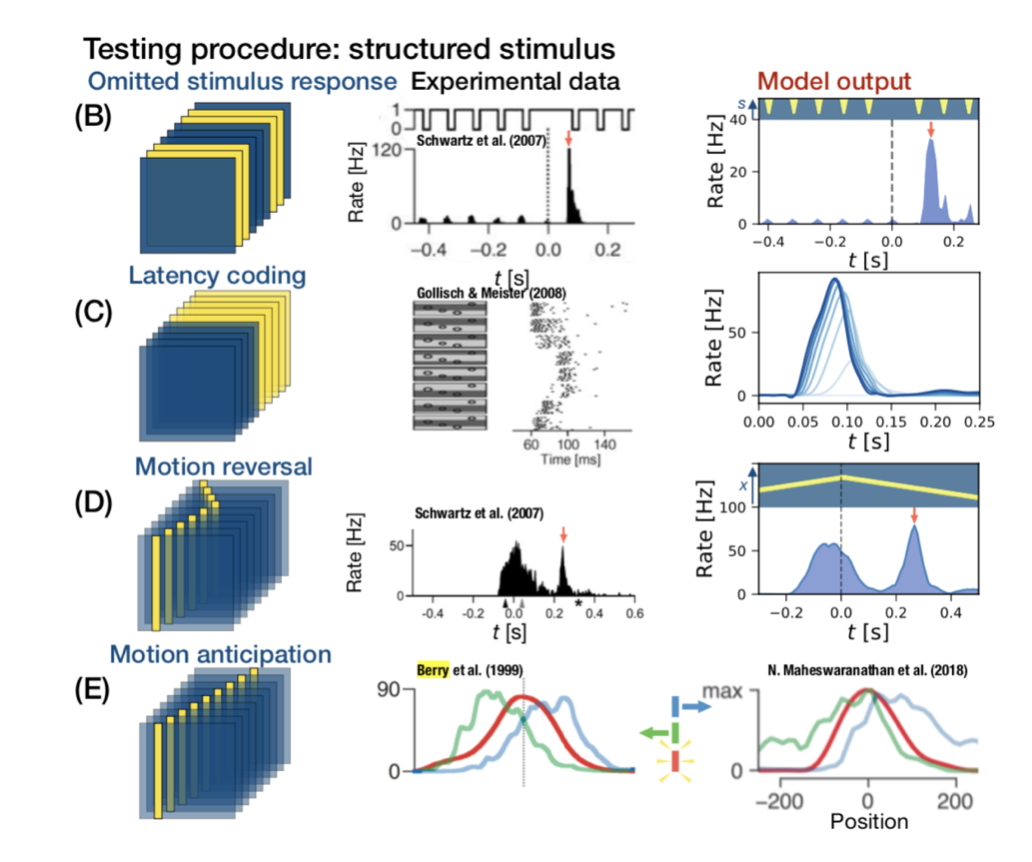
In this figure (from the preprint, but closely related to figure 4 from the neuron paper), the CNN trained on natural movies reproduces a myriad of predictive retinal behaviors that experimentalists have come up with over the years.

If the brain is constantly making predictions and comparing them with sensory input, shouldn’t we see signs of these predictions in neural activity? Shouldn’t there be massive feedback signals carrying predictions from higher brain areas to lower ones?

That’s just not what neuroscientists find. Even the staunchest proponents of feedback find small modulatory changes in firing rates in V1. When they looked for effects of feedback in visual processing, they find subtle modulations if anything. And most of these studies have very poor controls for the myriad of potential confounds in their results (such as changes in the retinal input from eye movements). It is fair to conclude that higher brain areas might slightly enhance or suppress activity in lower areas in a modulatory way, but not that they carry large predictions that are subtracted in the cell bodies of sensory neurons. TLDR: things look mostly like the standard model plus subtle modulation.

This is the puzzle we’re left with. Our best theories of perception tell us the brain must be doing some kind of inference, some kind of prediction. Our best theoretical framework for understanding the brain tells us the brain is a prediction machine. But our best measurements and models of brain activity show us something that looks a lot more like passive (albeit adaptive) feedforward* filtering.

*I’m using feedforward loosely here. I do include recurrent circuits in this definition. I am trying to contrast the idea that higher areas are feeding back detailed predictions. To date, the best models of visual cortical areas are feedforward CNNs or RNNs with no hierarchical feedback 8. Further, I’d argue that the “standard model” has evolved to include recurrent connections.

How do we resolve this? One possibility is that our theories of perception are just wrong. Maybe the brain really is just a fancy filter, and all that talk of inference and prediction is misguided. Or, all of the inference is simply embedded in the distribution of filters.

I don’t think either of those are the answer. The point I am arguing here is that “predictive coding” (or something slightly more general) provides a mathematical starting point (a framework) and the standard model is the answer for what inference looks like. You begin with a normative objective, but any theory worth its weight will find an answer that looks like the standard model in the steady state. In fact, this is where the roots of predictive coding lie: the earlierst work on predictive coding in the brain was about interpreting inhibition in the retina as prediction. It didn’t introduce some massive feedback of expectations, it simply changed the interpretation of the surround suppression in the retina.

Prediction Without Generating: Sparse Coding and the Locally Competitive Algorithm (LCA)

In the rest of this post I show that you can take the Generative Modeling perspective, do MAP inference over the latents of the model, and what falls out looks remarkably like the standard model. The model in question is sparse-coding inference scheme that was developed by Chris Rozell and Bruno Olshausen and can be implemented without ever forming an explicit “prediction” vector. Nevertheless, it still accomplishes the same job: inferring latent variables $z$ that explain the data $x$.

A Simple Generative Model

We start with a generative model of the form:

• $x\in {\mathbb{R}}^d$: The observed data (e.g., an image).
• $z\in {\mathbb{R}}^m$: Latent variables or “features.”
• $\Phi \in {\mathbb{R}}^{d\times m}$: A dictionary or set of “receptive fields.”
• $\epsilon$: Gaussian noise.
• ${\sigma }^2=1$: Noise variance is one for convenience later.

Under a sparsity prior (e.g., an $({\ell }_1)$ penalty on $(z))$, we can write the (negative) log-posterior (dropping additive constants) as:

This is the well-known sparse coding generative model proposed by Olshausen and Field. Importantly, altough it is a linear generative model, it is not a linear model, as you will see in the next section. What this model is saying is that the brain is trying to explain the input images, $x$, as a weighted combination of features, $\Phi$, plus some noise, $\epsilon$. As in most sparse coding schemes, the latents are penalized by a sparsity inducing prior. Basically, what this model is saying is “explain as much of the image as you can with as few active features as possible”.

Inference Without Explicit Predictions

In a typical predictive-coding approach, you might form the “prediction”, $\hat{x}=\Phi z$, and compute the error, $e=\hat{x}-x$. But let’s see how we can update $z$ without ever explicitly constructing $\hat{x}$.

Let’s look back at our loss function:

There are two tasks we need to perform: we need to learn the dictionary $\Phi$ and the latent variables $z$. Here, we will focus on updating $z$ while assuming that $\Phi$ has already been learned. In more neuroscience speak, this is our attempt to model perception. The brain has already learned its generative model, and now it needs to infer the latent variables that best explain the sense data, $x$. Note: yes, this is overly simplistic, but we can gain some powerful intuitions from it.

So, how do we set $z$ to minimize $\mathcal{L}(z)$? We can do this by taking the gradient of $\mathcal{L}(z)$ with respect to $z$ and updating $z$ in the direction of the negative gradient. This is a standard approach in optimization known as gradient descent. Combined with our sparsity-inducing Laplacian prior, this can be seen as MAP inference over the latents. In other words, this is one way to do inference over this generative model.

Below is a derivation of the gradient of $\mathcal{L}(z)$ (Note: technically it is the subgradient because of the ${\ell }_1$ term):

First term: For the term $\frac{1}{2{\sigma }^2}\Vert x-\Phi z{\Vert }_2^2$,

let $r(z)=x-\Phi z$. Then

Taking the gradient with respect to $z$:

Including the factor $\frac{1}{2{\sigma }^2}$ and take advantage of the fact that we set ${\sigma }^2=1$:

Second term: The ${\ell }_1$ term is

Its subgradient with respect to $z$ is

where $\mathrm{sign}(z)$ is applied element-wise:

Full Gradient Update Putting these together, the subgradient of $\mathcal{L}(z)$ at gradient update iteration $t$ is:

A simple gradient descent step with step size ${\eta }_z$ gives:

So, there we have it. The update rule for MAP inference over the Olshausen and Field sparse coding model. But Notice that this still has still has that $\Phi z^{(t)}$ term in it, meaning that the full prediction is present at every step. This updates the latents, $z$ with a weighted sum of the prediction error, ${\Phi }^{\top }{e}^{(t)}$, where $e=\Phi z-x$ is the prediction error.

But this is where the magic happens. Notice that multiplying out ${\Phi }^{\top }{e}^{(t)}$ removes the prediction term altogether:

This has a pretty interesting form. Nowhere does the full prediction exist. Instead, we can interpret these terms in neurally plausible ways.

• ${\Phi }^{\top }x$ acts like a feedforward drive (receptive field).
• ${\Phi }^{\top }\Phi$ is just a matrix, which acts like a set of recurrent (lateral) weights.

There is no prediction anymore. It’s just a good old-fashined recurrent neural network.

Starting from $z^{(0)}=0$ (all zeros) and iterating this update will (in many practical settings) drive $z$ toward a sparse solution, and the dynamics of $z$ naturally capture many of the extraclassical nonlinearities observed in V1. Rozell and colleagues implement sparsity with a thresholding operation that really takes equation to be closer to the standard model.

Crucially, nowhere in this update do we store $\Phi z^{(t)}$ as an explicit “prediction.” Yet functionally, the network is performing the same operation a predictive-coding model would and explains many of the extraclassical receptive field properties that made predictive coding impactful int he first place. Nowhere are we storing the full error term $e^{(t)}$ or the full “predicted image” $\hat{x}$ in a buffer. Further, because the learning of $\Phi$ results in sparse, localized, receptive fields, the lateral interactions between neurons are local in some sense. Notably, they are local in the pixel space of the input and topological constraints would need to be made on the latents themselves to make those things match eachother, but that’s kind of besides the point here. The key point is that a generative model can operate without generating and that gives us some sense of what to look for when building generative models.

Why This Matters

2. Neural Plausibility:
   There is limited evidence for detailed predictions being formed sent around in cortical circuits. On the other hand, there is evidence for strong feedforward receptive fields and extensive recurrent connectivity. The update rule we derived here shows that inference over a generative model can be realized using those two mechanisms alone.

3. Ruling out codes:
   This also shows us that our intuitions might be quite wrong until we “crank through the math”. I have to thank Bruno Olshausen and Christian Shewmake for pointing this out to me. The “standard model” camp regularly criticizes predictive coding, saying “yea, but we don’t see predictions and our feed-forward + recurrent models are the best”. But, here we ended up with a feedforward + recurrent model that is effectively doing (one-layer) predicive coding. The latent variables $(z)$ are being updated to better explain the data, without ever generating a separate “predicted” version of $(x)$.

Here’s the big deal: this is what I think we are looking for. Well, not this exactly. But I think many in the field are holding out hope that feedback is the main story in the brain and that the “standard model” is somehow wrong. I don’t think the empirical results will change. Feedback is weak modulation. The standard model is a good functional model of visual processing. It replicates. I’d go further to argue that any experimentalist that finds something that fundamentally violates the standard model didn’t control for something. Any theorist that proposes a theory that dramatically violates the standard model got the wrong answer.

The standard model is not a theory. It is a description of a large body of empirical descriptions. Theoretical approaches to understanding the brain have to start somewhere else – I think a great starting point is KL minimization, which subsumes all of machine learnin. But they should end up with something that closely resembles the standard model.

I’d further argue that it’s probably not worth trying to map a normative theory directly on to anything that doesn’t look somewhat like the standard model. What we want is a model that starts with hierarchical Bayesian inference and ends up with a spiking neural network with local connections and fairly coarse modulatory feedback. This exercise reveals to us that subtle changes in how we set up the problem and how we derive the answer can lead to very different conclusions. It may be very important to rethink some of the starting assumptions in the predictive coding literature (such as the gaussian assumption) that currently result in large addtive feedback signals.

So, what is feedback for?

It might very well be for inference under a generative model. But the form of it is a coarse modulation, not a subtractive prediction. I think we know that. I think we would benefit from acknowledging that is the case.

There are a lot of reasons the brain might need to use feedback for inference. I think the most likely is that it changes what information gets “out” of an area. Only some of the information in the activity of neurons in a brain area gets out. Modestly changing the gain of neurons can dramatically change what makes it through a hierarchy of areas. Li Zhaoping calls this querying and it’s an interesting perspective that fits nicely within inference.

Another possibility is that feedback is part of the “outer loop”. In our example above, I only ran MAP inference using gradient descent on the latents, $z$. This is our stand in for perception. However, there is no way with my simple model to make the predictions disappear when updating $\Phi$. That has to happen too, but even in our simulations, it usually happens on a slower timescale outside the perception loop. One crazy idea is that fMRI is reflecting the outer loop timescale, not just lowpassed spiking. If our model generates $x$ conditioned on both internal latents $z$ and some estimate of the body state $a$, then there are even more outer loops that might requrie feedback. All I’m saying here is maybe we know what inference looks like. In the steady state (i.e., for an image), it looks something like the standard model.

Appendix:

Experimental evidence

Although the field’s perspective on the feedforward view of visual cortex is changing in the last decade – with experimental results showing that motor signals are present in sensory areas ( 1, 2, 3) – I am very skeptical of generality these results, which we have repeatedly failed to replicate in primates ( 4, 5). I will cover the details of this in another post where I go into depth about why most of these results are likely the result of uncontrolled eye movements, which trivially change the retinal input, but in the meantime, you can read our perspective on the matter. For the purposes here, even with strong motor signals, attention, and decision signals, no one finds detailed visual predictions ( 7).